Reaction rate
The reaction rate (rate of reaction) or speed of reaction for a reactant or product in a particular reaction is intuitively defined as how fast or slow a reaction takes place. For example, the oxidation of iron under the atmosphere is a slow reaction that can take many years, but the combustion of butane in a fire is a reaction that takes place in fractions of a second.
Chemical kinetics is the part of physical chemistry that studies reaction rates. The concepts of chemical kinetics are applied in many disciplines, such as chemical engineering, enzymology and environmental engineering.
Contents |
Formal definition of reaction rate
Consider a typical chemical reaction:
- aA + bB → pP + qQ
The lowercase letters (a, b, p, and q) represent stoichiometric coefficients, while the capital letters represent the reactants (A and B) and the products (P and Q).
According to IUPAC's Gold Book definition[1] the reaction rate r for a chemical reaction occurring in a closed system under constant-volume conditions, without a build-up of reaction intermediates, is defined as:
where [X] denotes the concentration(Molarity, mol/L) of the substance X. (NOTE: Rate of a reaction is always positive. '-' sign is present in the reactant involving terms because the reactant concentration is decreasing.) The IUPAC[1] recommends that the unit of time should always be the second. In such a case the rate of reaction differs from the rate of increase of concentration of a product P by a constant factor (the reciprocal of its stoichiometric number) and for a reactant A by minus the reciprocal of the stoichiometric number. Reaction rate usually has the units of mol dm−3 s−1. It is important to bear in mind that the previous definition is only valid for a single reaction, in a closed system of constant volume. This most usually implicit assumption must be stated explicitly, otherwise the definition is incorrect: If water is added to a pot containing salty water, the concentration of salt decreases, although there is no chemical reaction.
For any system in general the full mass balance must be taken into account: IN - OUT + GENERATION = ACCUMULATION
When applied to the severe case stated previously this equation reduces to: ![r= \frac{d[A]}{dt}](/2012-wikipedia_en_all_nopic_01_2012/I/89b02377269a1560847a79cf1c684d28.png)
For a single reaction in a closed system of varying volume the so called rate of conversion can be used, in order to avoid handling concentrations. It is defined as the derivative of the extent of reaction with respect to time.
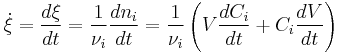
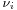 is the stoichiometric coefficient for substance
is the stoichiometric coefficient for substance  ,
, 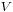 is the volume of reaction and
is the volume of reaction and 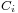 is the concentration of substance
is the concentration of substance  .
.
When side products or reaction intermediates are formed, the IUPAC[1] recommends the use of the terms rate of appearance and rate of disappearance for products and reactants, properly.
Reaction rates may also be defined on a basis that is not the volume of the reactor. When a catalyst is used the reaction rate may be stated on a catalyst weight (mol g−1 s−1) or surface area (mol m−2 s−1) basis. If the basis is a specific catalyst site that may be rigorously counted by a specified method, the rate is given in units of s−1 and is called a turnover frequency.
Factors influencing rate of reaction
- The nature of the reaction: Some reactions are naturally faster than others. The number of reacting species, their physical state (the particles that form solids move much more slowly than those of gases or those in solution), the complexity of the reaction and other factors can influence greatly the rate of a reaction.
- Concentration: Reaction rate increases with concentration, as described by the rate law and explained by collision theory. As reactant concentration increases, the frequency of collision increases.
- Pressure: The rate of gaseous reactions increases with pressure, which is, in fact, equivalent to an increase in concentration of the gas. For condensed-phase reactions, the pressure dependence is weak.
- Order: The order of the reaction controls how the reactant concentration (or pressure) affects reaction rate.
- Temperature: Usually conducting a reaction at a higher temperature delivers more energy into the system and increases the reaction rate by causing more collisions between particles, as explained by collision theory. However, the main reason that temperature increases the rate of reaction is that more of the colliding particles will have the necessary activation energy resulting in more successful collisions (when bonds are formed between reactants). The influence of temperature is described by the Arrhenius equation. As a rule of thumb, reaction rates for many reactions double for every 10 degrees Celsius increase in temperature,[2] though the effect of temperature may be very much larger or smaller than this.
For example, coal burns in a fireplace in the presence of oxygen, but it does not when it is stored at room temperature. The reaction is spontaneous at low and high temperatures but at room temperature its rate is so slow that it is negligible. The increase in temperature, as created by a match, allows the reaction to start and then it heats itself, because it is exothermic. That is valid for many other fuels, such as methane, butane, and hydrogen.
Reaction rates can be independent of temperature (non-Arrhenius) or decrease with increasing temperature (anti-Arrhenius). Reactions without an activation barrier (e.g., some radical reactions), tend to have anti Arrhenius temperature dependence: the rate constant decreases with increasing temperature.
- Solvent: Many reactions take place in solution and the properties of the solvent affect the reaction rate. The ionic strength also has an effect on reaction rate.
- Electromagnetic radiation and intensity of light: Electromagnetic radiation is a form of energy. As such, it may speed up the rate or even make a reaction spontaneous as it provides the particles of the reactants with more energy. This energy is in one way or another stored in the reacting particles (it may break bonds, promote molecules to electronically or vibrationally excited states...) creating intermediate species that react easily. As the intensity of light increases, the particles absorb more energy and hence the rate of reaction increases.
For example, when methane reacts with chlorine in the dark, the reaction rate is very slow. It can be sped up when the mixture is put under diffused light. In bright sunlight, the reaction is explosive.
- A catalyst: The presence of a catalyst increases the reaction rate (in both the forward and reverse reactions) by providing an alternative pathway with a lower activation energy.
For example, platinum catalyzes the combustion of hydrogen with oxygen at room temperature.
- Isotopes: The kinetic isotope effect consists in a different reaction rate for the same molecule if it has different isotopes, usually hydrogen isotopes, because of the mass difference between hydrogen and deuterium.
- Surface Area: In reactions on surfaces, which take place for example during heterogeneous catalysis, the rate of reaction increases as the surface area does. That is because more particles of the solid are exposed and can be hit by reactant molecules.
- Stirring: Stirring can have a strong effect on the rate of reaction for heterogeneous reactions.
All the factors that affect a reaction rate, except for concentration and reaction order, are taken into account in the rate equation of the reaction.
Rate equation
For a chemical reaction n A + m B → C + D, the rate equation or rate law is a mathematical expression used in chemical kinetics to link the rate of a reaction to the concentration of each reactant. It is of the kind:
In this equation k(T) is the reaction rate coefficient or rate constant, although it is not really a constant, because it includes all the parameters that affect reaction rate, except for concentration, which is explicitly taken into account. Of all the parameters described before, temperature is normally the most important one.
The exponents n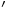 and m
and m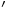 are called reaction orders and depend on the reaction mechanism.
are called reaction orders and depend on the reaction mechanism.
Stoichiometry, molecularity (the actual number of molecules colliding), and reaction order coincide necessarily only in elementary reactions, that is, those reactions that take place in just one step. The reaction equation for elementary reactions coincides with the process taking place at the atomic level, i.e. n molecules of type A colliding with m molecules of type B (n plus m is the molecularity).
For gases, the rate law can also be expressed in pressure units using, e.g., the ideal gas law.
By combining the rate law with a mass balance for the system in which the reaction occurs, an expression for the rate of change in concentration can be derived. For a closed system with constant volume, such an expression can look like
Temperature dependence
Each reaction rate coefficient k has a temperature dependency, which is usually given by the Arrhenius equation:
Ea is the activation energy and R is the gas constant. Since at temperature T the molecules have energies given by a Boltzmann distribution, one can expect the number of collisions with energy greater than Ea to be proportional to 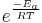 . A is the pre-exponential factor or frequency factor.
. A is the pre-exponential factor or frequency factor.
The values for A and Ea are dependent on the reaction. There are also more complex equations possible, which describe temperature dependence of other rate constants that do not follow this pattern.
Pressure dependence
The pressure dependence of the rate constant for condensed-phase reactions (i.e., when reactants and products are solids or liquid) is usually sufficiently weak in the range of pressures normally encountered in industry that it is neglected in practice.
The pressure dependence of the rate constant is associated with the activation volume. For the reaction proceeding through an activation-state complex:
the activation volume, 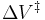 , is:
, is:
where 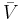 denote the partial molar volumes of the reactants and products and
denote the partial molar volumes of the reactants and products and 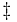 indicates the activation-state complex.
indicates the activation-state complex.
For the above reaction, one can expect the change of the reaction rate constant (based either on mole-fraction or on molar-concentration) with pressure at constant temperature to be:
In practice, the matter can be complicated because the partial molar volumes and the activation volume can themselves be a function of pressure.
Reactions can increase or decrease their rates with pressure, depending on the value of 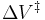 . As an example of the possible magnitude of the pressure effect, some organic reactions were shown to double the reaction rate when the pressure was increased from atmospheric (0.1 MPa) to 50 MPa (which gives
. As an example of the possible magnitude of the pressure effect, some organic reactions were shown to double the reaction rate when the pressure was increased from atmospheric (0.1 MPa) to 50 MPa (which gives 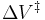 =-0.025 L/mol).[3]
=-0.025 L/mol).[3]
Examples
For the reaction
The rate equation (or rate expression) is:
The rate equation does not simply reflect the reactants stoichiometric coefficients in the overall reaction: It is first order in H2, although the stoichiometric coefficient is 2 and it is second order in NO.
In chemical kinetics, the overall reaction is usually proposed to occur through a number of elementary steps. Not all of these steps affect the rate of reaction; normally it is only the slowest elementary step that affect the reaction rate. For example, in:
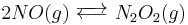 (fast equilibrium)
(fast equilibrium)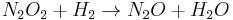 (slow)
(slow)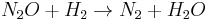 (fast)
(fast)
Reactions 1 and 3 are very rapid compared to the second, so it is the slowest reaction that is reflected in the rate equation. The slow step is considered the rate determining step. The orders of the rate equation are those from the rate determining step.
See also
- Reaction rate constant
- Rate equation
- Dilution (equation)
- Diffusion-controlled reaction
- Steady state approximation
- Collision theory and transition state are chemical theories that attempt to predict and explain reaction rates.
Notes
- ^ a b c IUPAC definition of rate of reaction
- ^ Kenneth Connors, Chemical Kinetics, 1990, VCH Publishers, pg. 14
- ^ Isaacs, N.S., "Physical Organic Chemistry, 2nd edition, Section 2.8.3, Adison Wesley Longman, Harlow UK, 1995.
External links
- Chemical kinetics, reaction rate, and order (needs flash player)
- Reaction kinetics, examples of important rate laws (lecture with audio).
- Rates of Reaction
- Overview of Bimolecular Reactions (Reactions involving two reactants)
![r = - \frac{1}{a} \frac{d[A]}{dt} = - \frac{1}{b} \frac{d[B]}{dt} = \frac{1}{p} \frac{d[P]}{dt} = \frac{1}{q} \frac{d[Q]}{dt}](/2012-wikipedia_en_all_nopic_01_2012/I/2cb2090fc10f8c18348e7fbea98ac4ef.png)
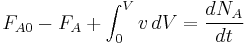
![\,r = k(T)[A]^{n'}[B]^{m'}](/2012-wikipedia_en_all_nopic_01_2012/I/493ba8a5537c9100593d9360d9a59543.png)
![\frac{d[C]}{dt} = k(T)[A]^{n'}[B]^{m'}](/2012-wikipedia_en_all_nopic_01_2012/I/73e873ab1b9e6162a0c45659b62d0b52.png)
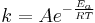
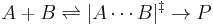
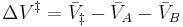
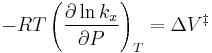
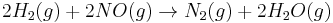
![r = k [H_2]^1[NO]^2 \,](/2012-wikipedia_en_all_nopic_01_2012/I/94762b015683b6e69622261518e9e6da.png)